 Tristan Kraft, H. Chau Nguyen und Otfried Gühne • 7/2022 • Seite 29 • DPG-Mitglieder
Tristan Kraft, H. Chau Nguyen und Otfried Gühne • 7/2022 • Seite 29 • DPG-MitgliederFerngesteuerte Quantensysteme
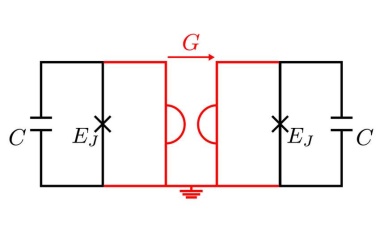
In der Quantenmechanik können Messungen an einem System ein anderes steuern.
In der Quantenmechanik lassen sich Teilchen an verschiedenen Orten durch eine gemeinsame Wellenfunktion beschreiben. In den 1930er-Jahren bemerkte Erwin Schrödinger, dass dies die Möglichkeit bietet, ein Quantensystem durch Messungen an einem weit entfernten weiteren System zu steuern. Seine Ideen waren jedoch lange vergessen und wurden erst in den letzten 15 Jahren wieder aufgegriffen. Mittlerweile ist es aber gelungen, die theoretisch vorhergesagten Effekte in Experimenten zu beobachten. Das Phänomen dieser Quantenkorrelation hängt eng mit anderen Konzepten wie der gemeinsamen Durchführbarkeit von Messungen zusammen und ist wichtig für Anwendungen wie die Quantenkryptographie.
Wenn zwei Tatverdächtige, Alice und Bob, bei einem Polizeiverhör dieselbe Geschichte erzählen, kann es dafür verschiedene Gründe geben. Alice kann von der Version Bobs erfahren haben und ihre Darstellung des Tatgeschehens danach ausgerichtet haben. Es kann aber auch eine gemeinsame Ursache für die Übereinstimmung geben. Im besten Fall erzählen Alice und Bob nichts als die Wahrheit. Die gemeinsame Ursache kann aber auch darin bestehen, dass sie sich im Vorhinein über eine Darstellung abgesprochen haben. Wenn die Verhöre gleichzeitig an verschiedenen Orten stattfinden, liegt eine gemeinsame Ursache nahe.
Was folgt, wenn die Antworten in dem Verhör auf eine gemeinsame Ursache zurückgehen? Dazu betrachten wir ein einfaches Modell: Alice und Bob bekommen Fragen gestellt (Waren Sie zur Tatzeit zuhause?) und geben eine von mehreren Antworten (ja oder nein). Etwas abstrakter lassen sich die Fragen an Alice durch einen Index x und die Antworten durch einen Index a beschreiben – bei Bob entsprechend durch y und b. Dann kann man sich die Wahrscheinlichkeiten anschauen, dass Alice a antwortet und Bob b, wenn Alice die Frage x und Bob die Frage y gestellt. (...)
 Guido Burkard • 4/2022 • Seite 24 • DPG-Mitglieder
Guido Burkard • 4/2022 • Seite 24 • DPG-MitgliederHalbleiter-Qubits voll funktionsfähig
Spin-Qubits auf Basis von Silizium zeigen eine vielversprechende Qualitätssteigerung.
 Sebastián A. Díaz und Karin Everschor-Sitte • 11/2021 • Seite 20 • DPG-Mitglieder
Sebastián A. Díaz und Karin Everschor-Sitte • 11/2021 • Seite 20 • DPG-MitgliederDer Quanten-Twist
Modellrechnungen haben gezeigt, dass sich kleine magnetische Skyrmionen als Qubit eignen.
 Philipp Schindler und Markus Müller • 10/2021 • Seite 35 • DPG-Mitglieder
Philipp Schindler und Markus Müller • 10/2021 • Seite 35 • DPG-MitgliederQuantenmessungen nach Maß
Maßgeschneiderte Quantensysteme erlauben es, komplexere Quantenmessungen zu realisieren und in der Quantentechnologie zu nutzen.
Die Messung einzelner Teilchen erlaubt es, charakteristische Vorhersagen der Quantenmechanik wie das Auftreten von Quantensprüngen in Quantenmessungen zu beobachten. Heute stehen kontrollierbare Quantensysteme zur Verfügung, in denen sich verschiedene Aspekte und Arten von Quantenmessungen gezielt realisieren und über weite Parameterbereiche maßschneidern lassen. Komplexere Messungen eröffnen die Möglichkeit, Fehler in Quantencomputern zu detektieren und zu korrigieren.
Messungen an individuellen Quantensystemen erfolgten erstmals in den 1980er-Jahren in Experimenten zum Nachweis diskreter Quantensprünge. Neuere Experimente erlauben es, über die kohärente Kopplung an Hilfssysteme allgemeinere Messungen zu implementieren und hierdurch die zeitliche Entwicklung der zu messenden Systeme zu untersuchen und zu beeinflussen.
Wir beginnen mit einer kurzen, abstrakten Einführung in einen Messapparat, der eine quantenmechanische Messung ermöglicht. Folgende Einschränkungen und Eigenschaften ergeben sich aus der Quantenmechanik:
- Die Quantentheorie kann im Allgemeinen nur eine statistische Aussage über Messergebnisse machen. Die Wahrscheinlichkeitsverteilung für einzelne Messergebnisse ist durch den klassischen Messapparat in Wechselwirkung mit dem zu messenden Quantensystem bestimmt. Die Quantentheorie formuliert diesen Zusammenhang.
- Eine Messung beeinflusst den Zustand des gemessenen Quantensystems. Das System befindet sich anschließend in dem Zustand, der dem Eigenzustand der Messobservablen entspricht. Bestimmte, nicht miteinander kompatible Messobservablen wie der Ort und die Geschwindigkeit eines Teilchens lassen sich meist nicht gleichzeitig beliebig genau messen (Unschärferelation). Bei aufeinanderfolgenden Messungen, wenn beispielsweise nach dem Ort auch die Geschwindigkeit gemessen wird, geht das System aufgrund der Rückwirkung der zweiten Messung in Bezug auf den Ort wieder in einen unbestimmten Zustand über.
Diese Axiome haben weitreichende Implikationen, insbesondere im Zusammenhang mit dem Gewinn und Verlust von Information. Im Allgemeinen ist der Gewinn von Information (der Erhalt eines Messergebnisses) mit der Kopplung an ein klassisches System verbunden. Dieser Vorgang ruft fast immer Dekohärenz hervor, die quantenmechanische Eigenschaften wie Verschränkung zerstört, die nicht im Rahmen klassischer Physik zu erklären sind. (...)
 Otfried Gühne und Guido Burkard • 3/2021 • Seite 3
Otfried Gühne und Guido Burkard • 3/2021 • Seite 3Mehr Kohärenz für die Quanteninformation
Ein neuer Fachverband der DPG bündelt Kompetenzen sektionsübergreifend.
 Oliver Morsch • 7/2018 • Seite 22
Oliver Morsch • 7/2018 • Seite 22Vereint verschränken, getrennt messen
In drei unabhängigen Experimenten gelang es, die Vielteilchenverschränkung in Bose-Einstein-Kondensaten nachzuweisen.
 Matthias Weidemüller • 10/2017 • Seite 22
Matthias Weidemüller • 10/2017 • Seite 22Rydbergs Baukasten für die Quantensimulation
Experimente mit riesigen Rydberg-Atomen erlauben die präzise Kontrolle
der dipolaren Wechselwirkung über mesoskopische Distanzen.
 Kai Bongs • 6/2017 • Seite 3
Kai Bongs • 6/2017 • Seite 3Initialzündung für Technologietransfer
Im Rahmen von Quantentechnologie-Hubs arbeiten in Großbritannien Grundlagenforscher eng mit der Industrie zusammen.
 Jonas N. Becker und Christoph Becher • 2/2017 • Seite 18
Jonas N. Becker und Christoph Becher • 2/2017 • Seite 18Ein Netzwerk aus Diamanten
Silizium-Fehlstellen-Farbzentren in Diamant-Mikrostrukturen ermöglichen integrierte Quantennetzwerke.
David Mesterhazy, Florian Hebenstreit und Uwe-Jens Wiese • 10/2016 • Seite 17Vielseitige Quantenbits
Ein 4-Qubit-Quantencomputer ermöglicht es, die Paarerzeugung von Teilchen und Antiteilchen zu berechnen.
 Mari Carmen Bañuls, J. Ignacio Cirac und Norbert Schuch • 9/2018 • Seite 43
Mari Carmen Bañuls, J. Ignacio Cirac und Norbert Schuch • 9/2018 • Seite 43Verschränkung und Information
Wie die Quanteninformationstheorie bei der Beschreibung von Quantenvielteilchensystemen hilft.
Quantenvielteilchensysteme weisen eine Vielzahl interessanter Phänomene auf, sind aber aufgrund ihrer komplexen Verschränkung sehr schwer zu modellieren. Ideen aus der Quanteninformationstheorie können uns helfen, solche Systeme mit Hilfe von Quantensimulatoren zu simulieren sowie basierend auf ihrer Verschränkungsstruktur effizient zu beschreiben.
Der enorme experimentelle Fortschritt in den letzten fünfzig Jahren hat viele grundlegende Tests der Quantenmechanik ermöglicht. Dies hat die Tür zu neuen Anwendungen aufgestoßen, insbesondere im Zusammenhang mit der Verarbeitung und Übertragung von Information. Quantencomputer und -kommunikationssysteme könnten das Gebiet der Informationsverarbeitung und Kryptographie revolutionieren, auch wenn die Konstruktion skalierbarer Geräte trotz erster Prototypen eine große Herausforderung darstellt. Mit diesen Bemühungen geht die Entwicklung einer Quantentheorie der Information einher, die beschreibt, wie sich die quantenmechanischen Gesetze nutzen lassen, um Daten effizient zu verarbeiten und zu übertragen. Zudem stellt diese Theorie eine formale Sprache zur Verfügung, um beliebige Quantensysteme zu beschreiben und viele Phänomene auf eine einheitliche Art zu verstehen. Diese Sprache hat sich über den Bereich der Informationsverarbeitung hinaus entwickelt und hält mittlerweile auch in andere Bereiche Einzug, wie die Atom-, Molekül- und Festkörperphysik, Optik und sogar Hochenergiephysik und Kosmologie.
 Wolfgang Pfaff • 2/2016 • Seite 20
Wolfgang Pfaff • 2/2016 • Seite 20Verschränkte Quanten im Wafer
Defekte in Siliziumkarbid könnten neue Quantentechnologien ermöglichen.
 Markus Greiner und Immanuel Bloch • 10/2015 • Seite 33
Markus Greiner und Immanuel Bloch • 10/2015 • Seite 33Quantengase unter dem Mikroskop
Neue Abbildungs- und Manipulationstechniken erlauben es, ultrakalte Quantengase
bis hin zu einzelnen Atomen zu beobachten und zu kontrollieren.
Festkörperphysikern wird es sicher auch in Zukunft versagt bleiben, jedes einzelne Elektron direkt beobachten, geschweige denn manipulieren zu können. Mit mesoskopischen Systemen aus ultrakalten Atomen statt Elektronen ist dieser Traum dank neuer Detektionstechniken jedoch Wirklichkeit geworden. Dies eröffnet eine Vielzahl neuer Möglichkeiten, um Quanten-Vielteilchensysteme zu charakterisieren und zu manipulieren. Die Anwendungen reichen von der Quantenoptik, Quanteninformation und Festkörperphysik bis zur Quantenfeldtheorie und statistischen Physik.
Die mikroskopische Anordnung und Bewegung von Elektronen in einem Festkörper bestimmt die makroskopischen Eigenschaften von Materialien. Oft ist dieser „Tanz“ der Elektronen hochkomplex und hochkorreliert, d. h. die Teilchen bewegen sich nicht unabhängig voneinander, sondern in einem komplexen Wechselspiel. Eine der großen fundamentalen Herausforderungen der Vielteilchenphysik in Quantensystemen besteht darin, diese Bewegung von Quantenteilchen zu verstehen und vorauszusagen. Als Experimentatoren wünschen wir uns dabei einen möglichst tiefen Einblick in dieses mikroskopische Quantentreiben und seine möglichst gute Kontrolle. Bislang gelang dies − höchst erfolgreich − durch immer bessere Mikroskope, vom Elektronenmikroskop über Rastertunnelmikroskope bis hin zu modernen kohärenten Röntgenquellen. Bisher versagt blieb es Experimentatoren jedoch, Schnappschüsse eines Festkörpers aufzuzeichnen, die jedes einzelne Elektron sichtbar machen. Eine solche „ultimative“ Beobachtung scheint unmöglich − in mesoskopischen Systemen ultrakalter Atome ist dieser Traum jedoch in den letzten Jahren Wirklichkeit geworden. Damit haben sich nicht nur neue Wege zur Charakterisierung von Quanten-Vielteilchensystemen ergeben, sondern auch neue Möglichkeiten zur Kontrolle über diese Systeme, angefangen von den elementarsten Bausteinen aus einzelnen Atomen.
Ausgangspunkt für die Experimente sind ultrakalte atomare Quantengase in künstlichen Kristallen aus Licht („optische Gitter“). Die Atome spielen die Rolle der Elektronen oder Cooper-Paare in einem Festkörper, dessen periodisches Ionengitter durch das optische Gitter ersetzt wird (Abb. 1). Durch Interferenz von Laserstrahlen lassen sich nahezu beliebige defektfreie Lichtgitter realisieren. Die Atome nehmen diese als Potentialgebirge wahr und können sich darin durch quantenmechanisches Tunneln von einem Gitterplatz zum nächsten bewegen. Zwei Gitterplätze in diesem optischen Kristall sind etwa 500 nm bis 1 μm voneinander entfernt, also etwa 10 000-Mal weiter als in einem typischen Festkörper. Dies erlaubt es prinzipiell, Atome in diesem künstlichen Festkörper optisch direkt zu detektieren, erfordert aber auch deutlich niedrigere Temperaturen, damit die de-Broglie-Materiewellenlänge groß genug wird, um eine Quantenentartung herzustellen. Typischerweise wechselwirken neutrale Atome nur lokal, also wenn sich zwei Atome auf einem Gitterplatz befinden. Dies sind die wichtigsten Zutaten des Hubbard-Modells, eines der prominentesten Modelle der Festkörperphysik für wechselwirkende Teilchen auf einem Gitter. Schon dieses einfache Modell zeigt ein reichhaltiges Phasendiagramm. Im Folgenden wollen wir uns auf bosonische Teilchen in einem Gitter konzentrieren und an diesem Beispiel zeigen, welche neuen Detektionsmöglichkeiten bisher Realität geworden sind.
 Gregor Weihs • 5/2015 • Seite 18
Gregor Weihs • 5/2015 • Seite 18Teleportation im Doppelpack
Mit einer technischen Meisterleistung ist es gelungen, Spin- und Bahndrehimpuls eines Photons auf ein anderes zu teleportieren.
 Rainer Blatt • 9/2012 • Seite 35
Rainer Blatt • 9/2012 • Seite 35Rechnen mit Quanten
In den letzten Jahren ist es gelungen, eine Reihe von Quantenzuständen
und einfachen Quantenalgorithmen zu realisieren.
In nicht allzu ferner Zukunft werden konventionelle Computer zwangsläufig an ihre Grenzen stoßen. Einen Ausweg könnten Quantencomputer bieten, die sich Superposition und Verschränkung zunutze machen. Quantencomputer mit einigen wenigen gespeicherten Ionen als elementaren Bausteinen liefern bereits heute vielversprechende Ergebnisse bei der Erzeugung nicht-klassischer Zustände sowie der Simulation von quantenmechanischen Systemen.
Seit Jahrzehnten verdoppelt sich etwa alle 18 Monate die Rechenleistung von Computern – empirisch beschrieben durch das Mooresche Gesetz, das einer der Gründungsväter der Firma Intel, Gordon Moore, 1965 formulierte. Seither folgt die Computertechnologie der dadurch vorgegebenen „roadmap“, vor allem durch fortschreitende Miniaturisierung, also immer kleinere Schaltelemente. Bei gleichbleibender Entwicklung müsste irgendwann im nächsten Jahrzehnt ein einzelnes Atom für die Darstellung eines Bits herhalten. Spätestens dann wäre es erforderlich, die Gesetze der Quantenphysik für das Rechnen heranzuziehen. Aber schon in den 1980er-Jahren überlegten David Deutsch und Richard Feynman, wie die Quantenphysik beim Rechnen helfen kann. Feynman hat als mögliche Anwendung zum Beispiel daran gedacht, die komplizierte Schrödinger-Gleichung eines Vielteilchensystems mithilfe eines anderen Quantensystems nachzubilden und zu simulieren, statt sie mühsam und unter großem Aufwand auf klassischen Computern zu berechnen. Dies waren damals aber rein akademische Überlegungen, da unklar war, ob und wie sich ein solcher Quantenrechner überhaupt realisieren ließe.
Als eigenständiges Forschungsfeld etablierte sich die Quanteninformationsverarbeitung ab Mitte der 1990er-Jahre. Auslöser dafür war die Entwicklung von Quantenalgorithmen, die eine sehr schnelle Lösung einiger wichtiger Probleme, wie die Faktorisierung großer Zahlen oder die Suche in Datenbanken, versprechen. Seither wurden verschiedenste Systeme für das Rechnen mit Quanten untersucht. Ignacio Cirac und Peter Zoller von der Universität Innsbruck schlugen 1995 einen der bislang erfolgreichsten Ansätze vor, der darauf beruht, Ionen in einer Paul-Falle zu manipulieren. Zwei interne Zustände der Ionen dienen dabei als Quantenbits (kurz Qubit), in denen die Quanteninformation gespeichert ist: |ψ〉 = c0 |0〉 + c1 |1〉. Die einzelnen Qubits lassen sich mithilfe von adressierten Laserstrahlen verarbeiten, wobei die Bewegung der Ionen in der Falle verwendet wird, um die logischen Gatteroperationen zwischen den Qubits zu erzeugen. Für den Bau eines universellen Quantencomputers reichen demnach zwei einfache Gatteroperationen und deren Kombinationen aus: Bei den sog. Ein-Qubit-Rotationen steuert man mit dem Laser gezielt einzelne Ionen an, während die zweite Operation das quantenmechanische Analogon eines Booleschen XOR-Gatters ist. Die klassische XOR-Operation invertiert ein Bit, wenn ein Kontroll-Bit gesetzt ist, d. h. sie involviert zwei Bits. Das quantenmechanische Analogon – die CNOT-Operation (controlled NOT) – unterscheidet sich davon fundamental, da es auch für Überlagerungen gelten muss und daher verschränkte Zustände erzeugt. Das entsprechende Zwei-Qubit-Gatter lässt sich ebenfalls mit Laserlichtimpulsen bestimmter Frequenz und Dauer unter Anregung der Ionenbewegung realisieren. Wichtig für diesen Ansatz ist, dass alle Ionen eines Quantenregisters stets in den Grundzustand der harmonischen Bewegung, die sie in dem Fallenpotential ausführen, zu kühlen sind. ...
 Piet O. Schmidt • 6/2012 • Seite 47
Piet O. Schmidt • 6/2012 • Seite 47Spektroskopie – aber logisch!
Die kohärente Manipulation von gefangenen Ionen ermöglicht die Präzisionsspektroskopie bislang unzugänglicher Spezies.
Optische Spektroskopie mit höchster Auflösung ist nur möglich an Atomen, die geeignete Übergänge zum Laserkühlen und zur Detektion des internen Zustands haben. Dies schränkte die Methode, z. B. im Hinblick auf hochgenaue Atomuhren, stark ein. Ein neues Verfahren, basierend auf Techniken der Quanteninformationsverarbeitung, hebt diese Beschränkung auf und macht eine Vielzahl weiterer Atome und Moleküle zugänglich. Das eröffnet faszinierende Möglichkeiten bei der Entwicklung optischer Uhren und bei Tests fundamentaler Theorien.
Präzisionsspektroskopie ist eine treibende Kraft für die Weiterentwicklung unseres physikalischen Verständnisses. So machten immer höhere spektroskopische Auflösungen Effekte wie die Fein- und Hyperfeinstruktur sowie die Lamb-Verschiebung sichtbar und führten zur Entwicklung der Quantenelektrodynamik (QED). Die QED ist einer der Grundpfeiler des sehr erfolgreichen Standardmodells der Teilchenphysik, das jedoch eine Reihe von Phänomenen, wie zum Beispiel Dunkle Materie bzw. Energie und die Asymmetrie in der Verteilung von Materie und Antimaterie, nicht erklären kann. Zudem ist die Gravitation nicht mit der QED vereinbar. Aus diesem Grund wird nach einer gemeinsamen Beschreibung aller fundamentalen Wechselwirkungen gesucht. Die Hoffnung besteht, dass die Spektroskopie mit immer höherer Auflösung irgendwann weitere Abweichungen von den Vorhersagen unserer besten Modelle liefert und damit die Richtung für eine verfeinerte und möglicherweise vereinheitlichte Theorie vorgibt.
Sehr lohnenswert ist hierbei die Untersuchung von Systemen, bei denen mögliche Abweichungen besonders ausgeprägt sind. Dazu zählen insbesondere spektroskopische Untersuchungen an Atomen und Molekülen, um mögliche Änderungen von Fundamentalkonstanten nachzuweisen, nach einem eventuellen Dipolmoment des Elektrons zu suchen, die Paritätsverletzung zu messen sowie generell die QED zu testen. Allerdings gibt es nur wenige theoretische Vorhersagen zur Größenordnung der zu erwartenden Effekte. Da diese im Labor noch nicht gefunden wurden, müssen die Abweichungen so winzig sind, dass nur höchstauflösende Methoden Erfolg versprechen.
Die mit Abstand genaueste Messmethode ist heutzutage die Laserspektroskopie, mit der sich Frequenzverhältnisse von optischen Uhren auf 17 Stellen genau angeben lassen. Dazu müssen die Referenzatome bestmöglich von störenden Umwelteinflüssen wie unerwünschten elektromagnetischen Feldern und Stößen mit anderen Atomen abgeschirmt sein. Paul-Fallen für Ionen im Ultrahochvakuum eignen sich dazu besonders gut, da sich die gefangenen Ionen dort in einem beinahe feldfreien Raum befinden. Durch den starken Falleneinschluss tritt bei der Spektroskopie praktisch kein Rückstoß auf (analog zum Mößbauer-Effekt), da ein einzelnes Photon den quantisierten Bewegungszustand des Ions in der Falle nicht ändert. ...
 Jürgen Lisenfeld und Alexey V. Ustinov • 4/2011 • Seite 21
Jürgen Lisenfeld und Alexey V. Ustinov • 4/2011 • Seite 21Verschränkte Photonenspeicher
Supraleitende Resonatoren haben großes Potenzial für die Quanteninformationsverbeitung.
Dietrich Leibfried • 12/2009 • Seite 45Ein Baukasten für Quanteningenieure
Quantencomputer sind nach wie vor Zukunftsmusik. Zwar ist es bereits gelungen, einfache Algorithmen zu implementieren, ein praxistauglicher Quantencomputer setzt jedoch eine skalierbare Quantentechnologie voraus, die es – analog zur gewöhnlichen Mikroelektronik – erlaubt, Quantenbits tausend- und millionenfach zu beherrschen. Ionenfallen sind hierfür ein vielversprechender Kandidat. Gleichzeitig ermöglichen sie Anwendungen über das ursprüngliche Ziel hinaus wie z. B. hochpräzise Uhren.
Markus Aspelmeyer • 4/2008 • Seite 19Quantenkommunikation mit Zwischenspeicher
Zwei neue Experimente zeigen einen Weg in Richtung Quantennetzwerke auf.
Arno Rauschenbeutel • 9/2007 • Seite 23
Schnittstelle für den Quantencomputer
Dieter Meschede • 9/2007 • Seite 47Atome mit Licht zähmen
Bereits seit einigen Jahren vollzieht sich sowohl in der Atomphysik als auch in der Quantenoptik eine spürbare Wandlung, die von der reinen Beobachtung der Phänomene wegführt. Inzwischen ist vielmehr der Wunsch, ein System präzise beeinflussen zu können, in den Mittelpunkt wissenschaftlicher Forschung gerückt. Die gezielte Manipulation von Quantensystemen ist dabei ein wesentlicher Schritt auf dem Weg zur Quanteninformationstechnologie – hier mit neutralen Atomen.
Christine Silberhorn • 9/2007 • Seite 61Laserlicht nach (Quanten-)Maß
Der Quantencharakter des Lichtes ermöglicht es, Information auf neuartige Weise sicherer und leistungsfähiger zu übertragen und zu verarbeiten. Die Konzepte der Quantenkommunikation- und -kryptographie basieren bislang auf Systemen mit diskreten Variablen, z. B. der Polarisation von Photonen. Doch Systeme mit kontinuierlichen Variablen versprechen große Übertragungsraten, und im diskret-kontinuierlichen Grenzbereich werden einfachere Bauelemente für die Verarbeitung von Quanteninformation erwartet.
Dagmar Bruß • 7/2007 • Seite 57Einführungen in die Quanteninformationstheorie
P. Kaye, R. Laflamme, M. Mosca: An Introduction to Quantum Computing
V. Vedral: Introduction to Quantum Information Science
Wolfgang Dür und Hans-J. Briegel • 12/2006 • Seite 22
Protokolle für die Quanteninformation
Rainer Blatt • 11/2005 • Seite 37Ionen in Reih und Glied
Ist eine Münze gezinkt oder nicht, d. h. weist sie Kopf und Zahl auf oder stimmen beide Seiten überein? Ein einfacher Quantenalgorithmus erlaubt es, diese Frage mit nur einem Blick auf die Münze statt zweien zu beantworten. Der ''Rechner'', auf dem dieser Algorithmus ausgeführt wird, besteht nicht aus Transistoren, sondern aus kalten, eingesperrten Ionen.
Gerhard Birkl • 11/2005 • Seite 45Atom-Chips, optische Gitter und Mikrolinsen
Nach den großen Erfolgen in der Quanteninformationsverarbeitung mit gespeicherten Ionen zeichnen sich vergleichbare Ergebnisse auch mit neutralen Atomen ab. Wie Ionen lassen sich Atome fast vollständig von der Umgebung abschirmen, und die verschiedenen Ansätze zur Implementierung atomarer Quantenprozessoren wie ''Atom-Chips'', Fallen aus Mikrolinsen oder optische Gitter versprechen eine hohe Flexibilität und Skalierbarkeit.
Gerd Schön und Alexander Shnirman • 11/2005 • Seite 51Qubits (fast) zum Anfassen
Bauelemente aus Festkörperstrukturen bieten für die Quanteninformationsverarbeitung mehrere Vorteile: Sie lassen sich schnell schalten, sie sind im Prinzip zu großen Systemen skalierbar und sie können in elektronische Kontroll- und Messkreise integriert werden. Allerdings führt die Kopplung an die externen Schaltkreise und die Umwelt auch zu Dekohärenz, deren Ursachen und Auswirkungen ein wesentlicher Schwerpunkt der aktuellen Forschung sind. Die größten Fortschritte wurden bislang mit Qubits erzielt, die auf Josephson-Kontakten beruhen.
J. Ignacio Cirac und Peter Zoller • 11/2005 • Seite 31Qubits, Gatter und Register
Zwar ist ein funktionierender Quantencomputer noch Zukunftsmusik, doch die theoretischen Grundlagen für seine Funktion, gewissermaßen sein Schaltplan, stehen bereit. Die Grundbausteine eines Quantencomputers lassen sich bereits mit gespeicherten Ionen oder mit neutralen Atomen in optischen Gittern realisieren. Letztere versprechen darüber hinaus die erste nichtriviale Anwendung der Quanteninformationsverarbeitung: die Simulation von bestimmten Vielteilchensystemen, die für klassische Computer unzugänglich sind.
Dagmar Bruß und Harald Weinfurter • 11/2005 • Seite 57Geheime Botschaften aus Licht
Durch die kommerzielle Bedeutung des Internet haben zuverlässige Methoden der Datenverschlüsselung Einzug in den Alltag gehalten. Ein gängiges Verschlüsselungsverfahren beruht darauf, dass es in endlicher Zeit kaum möglich ist, riesige Zahlen in ihre Primfaktoren zu zerlegen. Während es die Gesetze der Quantenmechanik im Prinzip erlauben, mit einem Quantencomputer dieses Verfahren zu knacken, liefern sie zugleich die Voraussetzungen für ein anderes, absolut sicheres Verschlüsselungsverfahren.
Dominik Janzing • 11/2005 • Seite 25Mit Quanten ist zu rechnen
Die Quantentheorie hat unzweifelhaft Physik und Technik revolutioniert und ebenso tiefschürfende Fragen in der Mathematik und Philosophie aufgeworfen. Mit dem Konzept des Quantencomputers erhält nun auch die Informatik neue Impulse. Die quantenmechanischen Gesetze erlauben nämlich grundsätzlich neuartige Ansätze, um Probleme zu knacken, für die auf klassischen Computern bislang kein effizientes Lösungsverfahren bekannt ist.
Dietrich Leibfried und Tobias Schätz • 1/2004 • Seite 23Ein atomarer Abakus
Ein Quantencomputer wäre dank der quantenmechanischen Überlagerung vieler Zustände in der Lage, Probleme zu lösen, welche die Kapazität selbst der größten konventionellen Hochleistungsrechner sprengen. Nachdem es zum Beispiel mit Ionen in Fallen bereits gelungen ist, einzelne Quanten-Rechengatter zu realisieren, besteht die Herausforderung nun in der Skalierung auf größere Rechner-Architekturen.
 • 7/2022 • Seite 29 • DPG-Mitglieder
• 7/2022 • Seite 29 • DPG-Mitglieder