Die Exponate des Gießener Mathematikums machen Mathematik auf unterhaltsame Weise erlebbar. (Bild: Mathematikum / Rolf K. Wegst, vgl. S. 26)


Die Exponate des Gießener Mathematikums machen Mathematik auf unterhaltsame Weise erlebbar. (Bild: Mathematikum / Rolf K. Wegst, vgl. S. 26)
Satellitenstart mit Verspätung / Obamas Klimainitiative / Forschung auf Autopilot
Zu: „Abbe ausgetrickst“ von J. Bewersdorf, Ch. Eggeling und T. A. Klar, Dezember 2014, S. 23 / Erwiderung von J. Bewersdorf, Ch. Eggeling und T. A. Klar
 • 3/2015 • Seite 18
• 3/2015 • Seite 18Die nichtlineare optische Anregung von Gitterschwingungen erlaubt es, die Sprungtemperatur von Hochtemperatur-Supraleitern kurzzeitig zu erhöhen.
 • 3/2015 • Seite 20
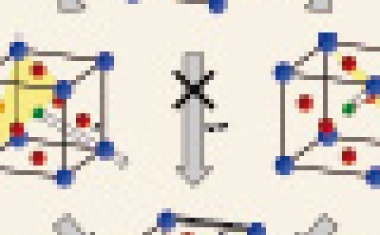
• 3/2015 • Seite 20In einem multiferroischen Schichtsystem lässt sich bei Zimmertemperatur die Magnetisierung mit einem elektrischen Feld umkehren.
 • 3/2015 • Seite 26
• 3/2015 • Seite 26Im Jahr 2002 eröffnete das Mathematikum in Gießen. Mathematikprofessor Albrecht Beutelspacher ist Initiator und Direktor und erhielt im vergangenen Jahr die Publizistikmedaille der DPG.
Erst ganz leise klirrt und klackert es – oben an der Decke hat sich wie von Geisterhand die große Kugelbahn in Bewegung gesetzt. Nach und nach werden bunte Kugeln in einer Art Fahrstuhl nach oben gehoben, von wo aus sie auf verschlungenen Wegen nach unten rollen. Fast schon wie Musik klingt es, wenn die Kugeln durch die Rohre rollen, durch Loopings rauschen, aber dann doch den Kampf gegen die Schwerkraft verlieren. In diesen wenigen Minuten, in denen die Kugeln sich bewegen, verstummen sämtliche Gespräche, und alle Blicke richten sich an die Decke. Nicht nur Kinder stehen staunend davor und bewundern dieses Schauspiel.
Diese übergroße Kugelbahn ist nur eines von rund 150 Exponaten des Gießener Mathematikums, des weltweit ersten Mathematikmuseums. Mathematik und Museum – das klingt nach einer Kombination, die eigentlich nicht funktionieren kann. Mathematik gilt als schwierig, ein Museum als langweilig. Das Projekt hätte von Anfang an zum Scheitern verurteilt sein müssen, sollte man meinen. Doch seit der Eröffnung im November 2002 kommen jährlich rund 150 000 Besucher in die Ausstellung. Angefangen hat alles im Jahr 1993, als der Gießener Mathematikprofessor Albrecht Beutelspacher „alles mal ganz anders machen wollte“. Und so gab er seinen Lehramtsstudenten für das Semester nur zwei Aufgaben: Baut ein geometrisches Objekt und erklärt die Mathematik dahinter. „Erst herrschte ziemliche Irritation“, erinnert sich Beutelspacher, „aber dann merkte ich, wie die Studenten sich mit dieser Aufgabe identifiziert haben und mit Begeisterung ans Werk gegangen sind.“ Ergebnis des Seminars waren nicht nur zufriedene Studenten mit vielen verschiedenen geometrischen Objekten, sondern die Idee, diese Möbius-Bänder, Platonischen Körper oder Tetraeder auch anderen Menschen zu zeigen. Im darauf folgenden Jahr wurden die Ergebnisse des Seminars in einem Raum der Universität gezeigt. Schnell sprach sich der Erfolg der Ausstellung herum, sodass Anfragen aus anderen Städten kamen. So gingen die Exponate 1995 erstmals auf Reisen, nämlich nach Nürnberg zur Tagung des Deutschen Vereins zur Förderung des mathematischen und naturwissenschaftlichen Unterrichts. Über Jahre hinweg wurde die Ausstellung weiterentwickelt und ergänzt und in weiteren Städten gezeigt. „Überall waren die Leute zunächst skeptisch, aber am Ende doch überwältigt“, erzählt Albrecht Beutelspacher. „Da war die Verlockung natürlich groß, aus der Ausstellung etwas Dauerhaftes zu machen.“
Als er im Jahr 2000 als erster den neu eingeführten Communicator-Preis des Stifterverbandes für die Deutsche Wissenschaft erhielt, war klar, dass die Idee der Mathematik-Ausstellung in der Öffentlichkeit angekommen ist. Die 100 000 DM Preisgeld steckte Beutelspacher komplett in die Realisierung des Mathematik-Museums. Hinzu kamen eine Finanzierung des Hessischen Wissenschaftsministeriums und eine EU-Finanzierung über das Wirtschaftsministerium. So konnte 2001 der Umbau des Gießener Hauptzollamts beginnen. Im November 2002 kam schließlich sogar der damalige Bundespräsident Johannes Rau zur Eröffnung und erlebte dort, wie viel Spaß Mathematik machen kann.
 • 3/2015 • Seite 31
• 3/2015 • Seite 31Starke Evidenzen sprechen dafür, dass die vor über 50 Jahren vorhergesagte FFLO-Supraleitung in starken Magnetfeldern tatsächlich auftritt.
Hohe Magnetfelder und Supraleitung vertragen sich üblicherweise nicht: Das Magnetfeld favorisiert parallel ausgerichtete Elektronenspins, während die Supraleitung Cooper-Paare mit antiparallelen Spins voraussetzt. Daher sollte bei ausreichend großen Feldern die Supraleitung zusammenbrechen. Wie Fulde und Ferrell sowie Larkin und Ovchinnikov bereits 1964 vorhergesagt haben, können räumlich getrennte supraleitende sowie magnetisch geordnete Bereiche aber auch bei noch höheren Magnetfeldern koexistieren.
In sehr vielen Metallen tritt bei tiefen Temperaturen das Phänomen der Supraleitung auf. Dabei fließt ein elektrischer Strom verlustfrei, wie Heike Kamerlingh Onnes 1911 an Quecksilber entdeckte. Erst 1957 gelang es jedoch John Bardeen, Leon Cooper und Robert Schrieffer, das Auftreten von Supraleitung mikroskopisch zu erklären. Im Rahmen der nach ihnen benannten BCS-Theorie führt eine beliebig kleine attraktive Wechselwirkung zwischen zwei Elektronen im Festkörper zur Bildung von Cooper-Paaren. Dabei wird die Gesamtenergie des elektronischen Systems im Festkörper abgesenkt, und Anregungen sind nur über eine Energielücke hinweg möglich. Die Größe dieser Energielücke bzw. auch die Dichte der Cooper-Paare sind ein Maß für die Stabilität des supraleitenden Zustands.
Magnetfelder unterdrücken die Supraleitung. Diese Beobachtung erwähnte Kamerlingh Onnes bereits 1913 auf dem „Third International Congress on Refrigeration“ in Chicago. Die prinzipielle Unverträglichkeit von Supraleitung und Magnetismus begrenzt bis heute die Anwendung von Supraleitung, um z. B. hohe Magnetfelder zu erzeugen. Allerdings sind inzwischen kritische Felder von weit über 100 Tesla möglich – eine enorme Steigerung gegenüber dem von Kamerlingh Onnes berichteten Wert von 0,05 Tesla. Diese hohen kritischen Felder treten in Materialien auf, in denen Supraleitung und Magnetismus einen Kompromiss eingehen und so in einem gewissen Bereich von Temperatur und Magnetfeld koexistieren. Charakteristisch für diese Kompromisszustände ist, dass die Supraleitung, genauer die Cooper-Paar-Dichte, inhomogen ist und in gewissen Bereichen auch verschwinden kann. Grob gesagt wird ein Teil des supraleitenden Volumens geopfert, um den supraleitenden Zustand zu erhalten. Ein typisches Beispiel dafür ist die Shubnikov-Phase, die sich in Typ-II-Supraleitern oberhalb eines unteren kritischen Feldes ausbildet. Charakteristisch für diese Phase sind periodisch angeordnete Flussschläuche mit normal leitenden Kernen, in die das Magnetfeld eindringt. Dabei entsteht ein Flussliniengitter, dessen Gitterkonstante von der Temperatur und vom Magnetfeld abhängt und das Experimente eindrucksvoll nachgewiesen haben.
 • 3/2015 • Seite 37
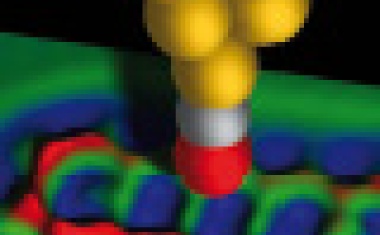
• 3/2015 • Seite 37Rasterkraftmikroskopie und die Philosophie des Abbildens.
In welchem Maße vermag die Rasterkraftmikroskopie, einzelne Atome abzubilden? Diese Frage zielt nicht nur auf den versierten Einsatz von Messgeräten. Vielmehr stellt sich dabei die grundsätzliche Problematik ein, was „Sehen“ und „Abbilden“ überhaupt heißen kann. Diesem konzeptuellen Problem können und sollten sich Physik und Philosophie gemeinsam stellen.
Sehen Sie Atome? Diese Frage stellte Hans-Joachim Güntherodt (1939 – 2014), der Basler Pionier der Rasterkraftmikroskopie, oft seinen Mitarbeitern beim Laborrundgang. Sie hatte nicht nur in den ersten Jahren nach der Einführung dieser experimentellen Methode ihre Berechtigung, sondern führt auf ganz grundsätzliche Aspekte. Diese lassen sich an einem aktuellen, sehr erfolgreichen Experiment diskutieren, bei dem ein einzelnes Pentacen-Molekül mit einem Rasterkraftmikroskop untersucht wird. In der Darstellung und Interpretation seines Ergebnisses (Abb. 1) greifen Schönheit der Darstellung, Klarheit der Aussage und konzeptionelle Verwirrung unmittelbar ineinander. Es stellen sich verschiedene Fragen, zum Beispiel ob die Einfärbung der Messergebnisse angemessen ist. Welchen Glauben an die Existenz von Atomen setzt es voraus, diese als schillernde Kugeln darzustellen? Ausgehend von diesen Fragen möchten wir hier zeigen, was Philosophen und Physiker in den gemeinsamen Blick nehmen können, um Grundsätzliches über Sehen und Abbilden in der Naturwissenschaft zu lernen.
Doch zunächst zur Funktionsweise eines Rasterkraftmikroskops: Dieses fährt mit einer extrem feinen Spitze mit einem Radius von nur wenigen Nanometern die zu untersuchende Oberfläche ab. Anhand der gemessenen Kräfte, die auf die Spitze wirken, lassen sich die Wechselwirkungen zwischen Spitze und Probe kartieren. Regelt man den Abstand der Spitze so nach, dass eine konstante Kraft wirkt, kann man eine Karte der Oberflächenform aufzeichnen. Im einfachsten Fall berührt die Spitze in Kontakt dabei die Probe. Die repulsiven Kräfte zwischen Spitze und Oberfläche sind über die Verbiegung einer mikroskopischen Blattfeder messbar, die an ihrem Ende die Spitze trägt. Die Spitze fährt also im repulsiven Kontakt die Form der Oberfläche nach. Das Ergebnis der Messung ist eine Zahlenmatrix, welche die vertikale Position der Spitze als Funktion ihrer lateralen Position angibt. Daraus wird ein Bild erzeugt, in dem die vertikale Position als Farbe kodiert ist. Typische Farbskalen weisen höheren Zahlenwerten hellere Farbtöne zu. Kontraste werden eingestellt, indem der Farbverlauf an die Verteilung der gemessenen Höhenwerte angepasst wird. Der Farbverlauf ist in der Regel so gewählt, dass die topographischen Kontraste gut zu erkennen sind. Teilweise sind die Ergebnisse auch als berechnete Projektion einer dreidimensionalen Fläche dargestellt, wobei durch Beleuchtungs- und Schattierungseffekte Details der Topographie noch deutlicher hervortreten (Abb. 1 und Beispiel im Infokasten).
 • 3/2015 • Seite 45
• 3/2015 • Seite 45Von der kosmologischen Konstante zur Dunklen Energie.
Mit seiner Allgemeinen Relativitätstheorie entwickelte Einstein vor hundert Jahren eine völlig neue Sicht auf Raum, Zeit und Gravitation. Bereits zwei Jahre danach schlug er ein kosmologisches Modell vor, das zwar nach einem Jahrzehnt überholt war, jedoch unerwartete Entwicklungen auslöste. Insbesondere zeigte sich, dass Raum und Zeit unweigerlich an der kosmischen Dynamik beteiligt sind. Mit dieser sind tiefliegende Rätsel zu Tage getreten, die für die Kosmologie und die Grundlagenphysik von größter Bedeutung sind.
Etwa ab dem Jahr 2000 haben Astronomen mit zunehmender Gewissheit nachgewiesen, dass das Universum seit langer Zeit beschleunigt expandiert.1) Seither ist die Diskussion um Einsteins kosmologische Konstante erneut entfacht worden und hat sich zum Problem der „Dunklen Energie“ ausgeweitet. Die Geschichte um diese Konstante ist nicht nur wechselvoll und interessant, vom Standpunkt der Quantentheorie aus ist ihre tatsächliche Kleinheit auch ein großes Rätsel. Eine befriedigende Deutung ist nicht in Sicht und wohl erst auf der Basis eines einheitlichen Verständnisses der fundamentalen Wechselwirkungen zu erhoffen. Es sei aber schon jetzt betont, dass in den Feldgleichungen der Allgemeinen Relativitätstheorie − einer klassischen Feldtheorie − zwei Konstanten frei sind und experimentell, also durch Beobachtungen, bestimmt werden müssen. Die Werte beider Konstanten sind sehr merkwürdig: Die Newtonsche Konstante G definiert eine riesig hohe Massenskala, die Planck-Skala von etwa 1019 Protonenmassen, während umgekehrt die kosmologische Konstante Λ eine Energie-Massendichte definiert, die vom Standpunkt der Elementarteilchenphysik aus gesehen winzig ist.
Die abstoßende Gravitation
In der schlimmsten Zeit des ersten Weltkrieges, am 8. Februar 1917, hielt Einstein vor der Preußischen Akademie der Wissenschaften einen Vortrag über die Anwendung seiner Allgemeinen Relativitätstheorie auf das gesamte Universum. Ein paar Tage vor seinem Referat schrieb er seinem Freund und Kollegen Paul Ehrenfest nach Leiden: „Ich habe wieder etwas verbrochen in der Gravitationstheorie, was mich ein wenig in Gefahr bringt, in ein Tollhaus interniert zu werden.“
Interview mit Wolfgang Baumjohann
WE Heraeus-Sommerschule und 20. Doktorandenschule „Saalburg“.