Glas vibriert anders

Manchmal ist das Wissen schon da – es wurde nur übersehen. Seit rund einem halben Jahrhundert rätseln Physiker über Vibrationen in Gläsern bei tiefen Temperaturen. Der Grund: Gläser tragen Schallwellen und Vibrationen anders weiter als andere Festkörper, sie schwingen anders. Nur warum? Und wie lässt sich die Ausbreitung von Schall in Gläsern korrekt berechnen? Matthias Fuchs und Florian Vogel von der Uni Konstanz haben jetzt die Lösung gefunden – indem sie ein altes Modell, das vor etwa zwanzig Jahren entstand und damals von der Fachwelt verworfen wurde, aufgriffen und neu ausarbeiteten.

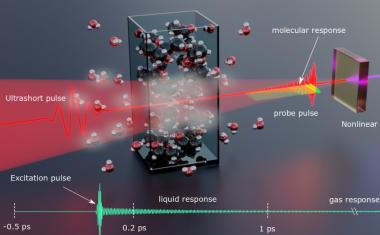
Sendet man Schallwellen durch ein Glas so stellt man eine gewisse Dämpfung der Schwingungen fest, die in anderen Festkörpern fehlt. Sie hat weit­reichende Konsequenzen für die thermischen Eigen­schaften von Gläsern wie Wärme­über­tragung und Wärme­kapazitäten. Der Effekt ist in der Physik wohlbekannt, nur gab es bislang kein theoretisches Modell, das ihn korrekt beschreibt – und den Rahmen für komplexere Berechnungen der Schall­aus­breitung in Gläsern bilden könnte.

Gläser sind ungeordnete Festkörper. Anders als bei kristallinen Festkörpern sind die Teilchen, aus denen Gläser bestehen, nicht regelmäßig angeordnet. Bei den meisten Festkörpern sitzen die Teilchen nahezu perfekt in Reih und Glied – wie Bausteine, die in einem präzisen Raster angeordnet wurden. Wenn solche kristallinen Festkörper bei tiefen Temperaturen zum Schwingen gebracht werden, geben die Teilchen die Schwingung ungedämpft an ihre Nachbarn weiter. Die Schwingung wird in einer gleich­förmigen Welle unvermindert weiter­getragen.

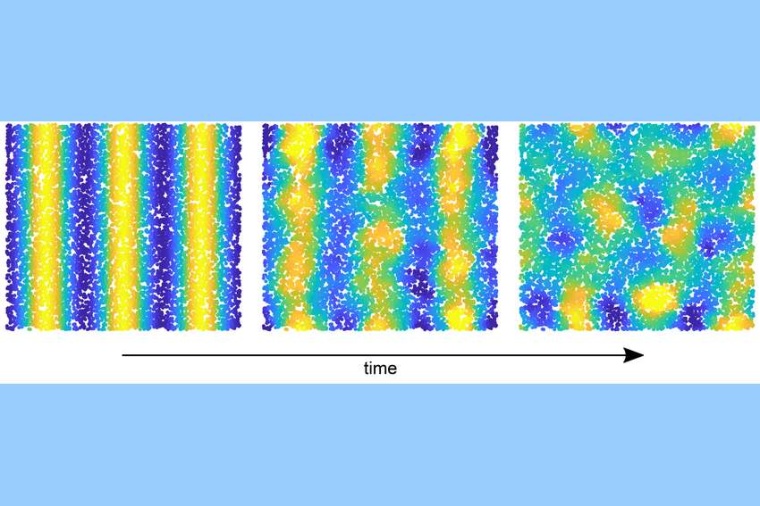
Nicht so bei Gläsern: Ihre Teilchen sitzen nicht in einem regel­mäßigen Raster, sondern auf zufälligen Positionen ohne stringente Ordnung. Wenn hier nun die Welle einer Schwingung ankommt, dann wird sie nicht in einem gleich­förmigen Muster weiter­getragen. Stattdessen wird die Schwingung an den zufälligen Positionen, an denen die Teilchen sitzen, aufgenommen und in einem entsprechend zufälligen Muster weiter­getragen.

Der Effekt: Die einheitliche Welle wird gebrochen und zerstreut sich in mehrere kleinere Wellen. Dieser Zerstreuungs­effekt verursacht die Dämpfung. Vor etwa zwanzig Jahren haben Marc Mezard, Giorgio Parisi, Anthony Zee und Kollegen diese Anomalien in Gläsern durch ein Modell von Schwingungen in zufälligen Positionen mithilfe des „Euclidean Random Matrix Approach“ beschrieben. „Ein einfaches Modell, mit dem sie die Lösung eigentlich schon in der Hand hielten“, so Fuchs. Das Modell hatte jedoch noch einige Ungereimt­heiten und wurde daher von der Fachwelt verworfen – und geriet in Vergessenheit.

Fuchs und sein Mitarbeiter Vogel griffen das alte Modell wieder auf. Sie lösten die offenen Fragen, die die Fachwelt damals unzufrieden ließen, und unter­suchten das über­arbeitete Modell durch Betrachtung seiner Feynman-Diagramme. Diese nützlichen Grafiken wurden von Richard Feynman in der Quanten­feld­theorie eingeführt und offenbarten die Gesetz­mäßig­keiten in den Mustern der gestreuten Wellen. Die Ergebnisse von Fuchs und Vogel lieferten realgetreue Berechnungen der Schall­aus­breitung und des Dämpfungs­effekts in Gläsern. „Mezard, Parisi und Zee lagen mit ihrem ein­sichtigen Modell richtig – harmonische Schwingungen in einem ungeordneten Arrangement erklären die Anomalien von Gläsern bei tiefen Temperaturen“, so Fuchs.

Mit dem neuen Modell ist die Geschichte um Vibrationen in Gläsern jedoch längst nicht abgeschlossen: „Für uns ist es der Einstieg: Wir haben jetzt das richtige Modell gefunden, mit dem wir weitere Berechnungen, besonders von quanten­mechanischen Effekten, anstellen können“, gibt Fuchs einen Ausblick.

U. Konstanz / RK

Weitere Infos

• Originalveröffentlichung
  F. Vogel & M. Fuchs: Vibrational Phenomena in Glasses at Low Temperatures Captured by Field Theory of Disordered Harmonic Oscillators, Phys. Rev. Lett. 130, 236101 (2023); DOI: 10.1103/PhysRevLett.130.236101
• Soft Condensed Matter Theory (M. Fuchs), FB Physik, Universität Konstanz